Modélisation des systèmes de mise à la terre : de l'état stable au transitoire

Plongez dans le comportement complexe des systèmes de mise à la terre aux hautes fréquences. Découvrez comment l'impédance change, comment les réponses transitoires apparaissent et comment les techniques de modélisation efficaces sont cruciales pour des performances optimales.

Publié le 22 juillet 2024600+ Vues5 min de lecture

Modélisation des systèmes de mise à la terre : de l'état stable au transitoire

Une conception appropriée des systèmes de mise à la terre est un facteur clé pour garantir le bon fonctionnement des réseaux électriques en termes de sécurité des personnes, de protection des composants, de coordination de l'isolation et de compatibilité électromagnétique (CEM). Les performances du système de mise à la terre en régime statique (basse fréquence) et dynamique (haute fréquence) sont importantes. En régime statique, l'objectif de la conception des systèmes de mise à la terre est de fournir la résistance de mise à la terre souhaitée, la montée du potentiel de terre, les tensions de contact et de pas en conditions de fonctionnement normales et après les courants de court-circuit [1] et [2]. L'analyse basse fréquence des systèmes de mise à la terre peut être effectuée soit en utilisant des formules empiriques, soit en utilisant des méthodes électromagnétiques numériques formulées en régime statique. Cependant, ces méthodes ne permettent pas d'obtenir des résultats précis aux hautes fréquences lorsqu'elles sont utilisées pour le calcul des surtensions générées par la foudre, en particulier pour les grands systèmes de mise à la terre où l'hypothèse d'équipotentialité pour les conducteurs de terre est violée. À la place, l'analyse haute fréquence des systèmes de mise à la terre est généralement réalisée en utilisant des méthodes électromagnétiques numériques rigoureuses. En régime haute fréquence, l'objectif de la conception du système de mise à la terre est de contrôler les surtensions générées par la foudre et également d'atténuer les différences de tension entre les différentes parties du système de mise à la terre soumises au courant de foudre. Il est à noter que les perturbations de tension transitoires dans les systèmes de mise à la terre peuvent entraîner des dysfonctionnements des instrumentations à faible signal en modifiant le point de référence de tension.

Les courants d'impulsion de foudre sont généralement caractérisés par une large bande de fréquences, de CC à plusieurs MHz, sur laquelle le système de mise à la terre présente un comportement différent à différentes fréquences. Par conséquent, pour obtenir des surtensions générées par la foudre précises, il faut tenir compte de la dépendance en fréquence des systèmes de mise à la terre.

électrodes de mise à la terre

Le concept de comportement transitoire des systèmes de mise à la terre peut être correctement décrit en évaluant le comportement basse et haute fréquence des électrodes de mise à la terre simples. Comme on le sait, les systèmes de mise à la terre à basse fréquence présentent un comportement résistif, de sorte qu'ils peuvent être raisonnablement modélisés par leur résistance CC. L'hypothèse électromagnétique de base à basse fréquence est de considérer les conducteurs de mise à la terre comme étant équipotentiels (en négligeant le délai de propagation) lorsqu'ils sont excités par le courant de court-circuit. Bien que cette hypothèse soit violée lorsque la taille de l'électrode de terre devient comparable à la longueur d'onde du courant d'excitation, il est toujours acceptable de modéliser les systèmes de mise à la terre par leur résistance CC aux basses fréquences. À cette fin, diverses méthodes telles que les méthodes électromagnétiques numériques avec des hypothèses statiques ou quasi-statiques [3], des expressions empiriques sous forme fermée [4]. Il est à noter cependant que les expressions sous forme fermée ne sont disponibles que pour les électrodes de terre verticales et horizontales simples.

Aux hautes fréquences, cependant, le comportement du système de mise à la terre est plus complexe et ne peut pas être modélisé avec précision à moins d'utiliser des méthodes de résolution électromagnétiques rigoureuses. En fait, dans de nombreuses études, il est prévu d'évaluer les performances des systèmes de mise à la terre sur une large bande de fréquences, de CC à plusieurs MHz. En pratique, la fréquence maximale d'intérêt est dictée par le type d'analyse particulière et la nature de la source de perturbation. Jusqu'à présent, les systèmes de mise à la terre ont été modélisés par différentes méthodes telles que la théorie des circuits [5] -[6], la théorie des lignes de transmission [7]-[9], et les approches en ondes complètes telles que la méthode des différences finies dans le domaine temporel (FDTD), la méthode des éléments finis (FEM) [10], et la méthode des moments (MoM) [11]-[16]. Les méthodes basées sur les circuits et la théorie des lignes de transmission sont considérées comme des approches quasi-statiques, qui échouent généralement à prédire le comportement haute fréquence des systèmes de mise à la terre. Les trois dernières méthodes (c'est-à-dire FDTD, FEM et MoM) peuvent être classées comme des approches en ondes complètes ou en champ électromagnétique, avec la possibilité d'évaluer avec précision les performances des systèmes de mise à la terre sur une large bande de fréquences.

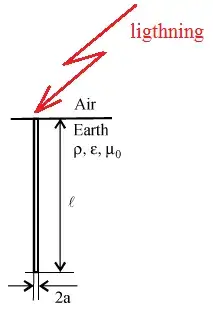
Fig. 1. Foudre frappant une électrode de terre verticale.

Pour mieux comprendre le comportement haute fréquence des systèmes de mise à la terre, considérons le cas d'une foudre frappant une électrode de terre verticale de longueur l = 3 m et d'une section transversale circulaire de rayon r = 12,5 mm, enterrée dans un sol de conductivité σ0 et de permittivité relative $\eps_r$ , Fig. 1. Un courant de 1 A est injecté dans le système de mise à la terre à chaque fréquence et l'impédance harmonique Z(jω) du système de mise à la terre est calculée en fonction de la fréquence,

Z(j \omega) = \frac{V(j \omega)}{I(j \omega)}

où V(jω) et I(jω) sont respectivement le vecteur de potentiel électrique au point d'alimentation par rapport à la terre lointaine et le vecteur du courant injecté [14]. Le potentiel électrique est calculé en intégrant le champ électrique le long d'un chemin rectiligne partant de la surface du conducteur de l'électrode jusqu'à un point très éloigné du point d'injection où le courant tend vers zéro et peut être considéré physiquement comme un point de référence de tension. La figure 3.2 montre l'amplitude et la phase de l'impédance harmonique de l'électrode de mise à la terre verticale, calculée à l'aide de l'approche FEM. L'analyse est réalisée pour quatre conductivités du sol différentes (c'est-à-dire σ0 = 0,01 S/m, 0,002 S/m, 0,001 S/m, 0,0005 S/m) ayant la même permittivité relative de $\eps_r$ = 20. Comme on peut le voir sur ces courbes, l'impédance harmonique varie sur la plage de fréquences de travail. Dans la plage de basses fréquences, l'amplitude de l'impédance harmonique est égale à la résistance statique (également appelée résistance CC) tandis qu'elle prend des valeurs différentes pour les fréquences plus élevées. Ce comportement des électrodes de mise à la terre est bien connu et a été largement discuté (par exemple, [14] et [16]). Ceci est assez différent du modèle statique du système de mise à la terre qui ne permet pas d'obtenir des résultats précis aux hautes fréquences lorsqu'il est utilisé pour le calcul des surtensions du système de mise à la terre. Dans un autre cas de simulation, la même électrode de mise à la terre verticale avec une longueur différente de l = 30 m est analysée. L'amplitude et la phase de l'impédance harmonique de cette électrode de mise à la terre sont présentées à la figure 2. Un examen plus approfondi de cette figure révèle que le comportement inductif ou capacitif des électrodes de mise à la terre est principalement déterminé par les paramètres électriques du sol ainsi que par la longueur de l'électrode. Comme on peut le voir à la figure 3, aux fréquences plus élevées et pour les sols hautement conducteurs, le comportement inductif est dominant. Il est assez différent du cas précédent où l'électrode de mise à la terre présente un comportement capacitif sur la plage de fréquences d'intérêt. Ce comportement est conforme à notre attente d'un comportement capacitif des électrodes de mise à la terre de petite et de moyenne longueur enterrées dans des sols peu conducteurs par rapport aux longues électrodes de mise à la terre [16]. La fréquence à laquelle l'impédance harmonique s'écarte de la résistance CC et passe à un comportement inductif ou capacitif est appelée fréquence caractéristique.

Impédance harmonique à la terre pour une tige de mise à la terre verticale de longueur l = 3 m et de section transversale circulaire de rayon r = 12,5 mm [14].

Fig. 2. Impédance harmonique à la terre pour une tige de mise à la terre verticale de longueur l = 3 m et de section transversale circulaire de rayon r = 12,5 mm [14].

Impédance harmonique à la terre pour une tige de mise à la terre verticale de longueur l = 30 m et de section transversale circulaire de rayon r = 12,5 mm [14].

Fig. 3. Impédance harmonique à la terre pour une tige de mise à la terre verticale de longueur l = 30 m et de section transversale circulaire de rayon r = 12,5 mm [14].

Fig. 4. Comportement de la dépendance en fréquence de l'impédance du système de mise à la terre. Adapté de [17].

La figure 4 montre un comportement typique de la dépendance en fréquence de l'impédance du système de mise à la terre. Sur cette figure, l'impédance harmonique |Z(jω)| est normalisée en étant divisée par la résistance basse fréquence à la terre Rg. À partir de cette figure et en se référant aux termes de circuit, le système de mise à la terre peut se comporter comme : i) un circuit capacitif dominant (|Z(jω)|/Rg < 1), ii) un circuit résistif (|Z(jω)|/Rg = 1) ou iii) un circuit inductif (|Z(jω)|/Rg > 1). L'impédance est presque constante dans la plage de basses fréquences tandis qu'elle présente un comportement dépendant de la fréquence aux hautes fréquences. Ces deux régions sont distinguées par la fréquence caractéristique Fc [17].

Dans la conception des systèmes de mise à la terre, les comportements résistif et capacitif sont plus préférables car l'impédance HF prend des valeurs égales ou inférieures à la résistance BF. Le comportement capacitif est typique des électrodes de terre courtes enterrées dans des sols très résistants. La figure 5 donne les régions de comportement inductif et capacitif des électrodes de terre verticales et horizontales en fonction de la longueur, de la résistivité de la terre et du point de décharge [17]. Il faut faire attention à la valeur de la résistance CC lorsque l'objectif est de réduire la valeur HF de l'impédance harmonique en réduisant la longueur de l'électrode. En fait, ce ne serait pas un choix pratique car il pourrait être en contradiction avec les valeurs souhaitées de la résistance CC, car elle nécessite généralement des électrodes plus longues.

Fig. 5. Comportement des électrodes de terre en fonction de la longueur de l'électrode et de la résistivité du sol. Adapté de [17]

Évaluation du comportement transitoire des électrodes de terre

Certains paramètres sont généralement définis pour caractériser le comportement transitoire des systèmes de mise à la terre. Après avoir calculé l'impédance harmonique des systèmes de mise à la terre, c'est-à-dire Z(jω), la fonction temporelle de la tension à la terre (tension transitoire) au point d'injection v(t) peut être facilement calculée en appliquant le courant de foudre i(t),

v(t) = F^{-1} \{ Z(j \omega) \cdot F \{ i(t) \} \}

où F et F-1 désignent respectivement les transformées de Fourier et de Fourier inverse.

L'impédance d'impulsion z0(t) est définie comme le rapport de la tension dans le domaine temporel au point d'injection au courant injecté [17] :

Z_0(t) = \frac{V(t)}{i(t)}

Alternativement, l'impédance d'impulsion conventionnelle Z peut être utilisée. Cette impédance est définie comme le rapport de la valeur maximale de v(t) à la valeur crête du courant injecté i(t) :

Z = \frac{\max[V(t)]}{\max[i(t)]} = \frac{V_{\max}}{I_{\max}}

L'efficacité d'impulsion est définie comme le rapport entre l'impédance conventionnelle et la résistance basse fréquence Rg, c'est-à-dire Efficacité d'impulsion = Z / Rg.

Il convient de mentionner que de meilleures performances d'impulsion sont associées à une valeur inférieure de l'efficacité d'impulsion.

Pour une électrode de mise à la terre verticale soumise à un courant de foudre de retour consécutif (Fig. 6), l'impédance d'impulsion en fonction de la longueur de l'électrode est présentée à la figure 7 pour différentes valeurs de conductivité du sol (c'est-à-dire σ0 = 0,01, 0,002, 0,001 S/m) ayant la même permittivité relative de $\eps_r$ . On constate également que plus l'électrode est longue, plus l'impédance d'impulsion est faible. Cependant, cet effet de réduction de la longueur de l'électrode sur l'impédance d'impulsion est limité par la longueur effective de l'électrode ; une longueur au-delà de laquelle l'impédance d'impulsion ne varie plus.

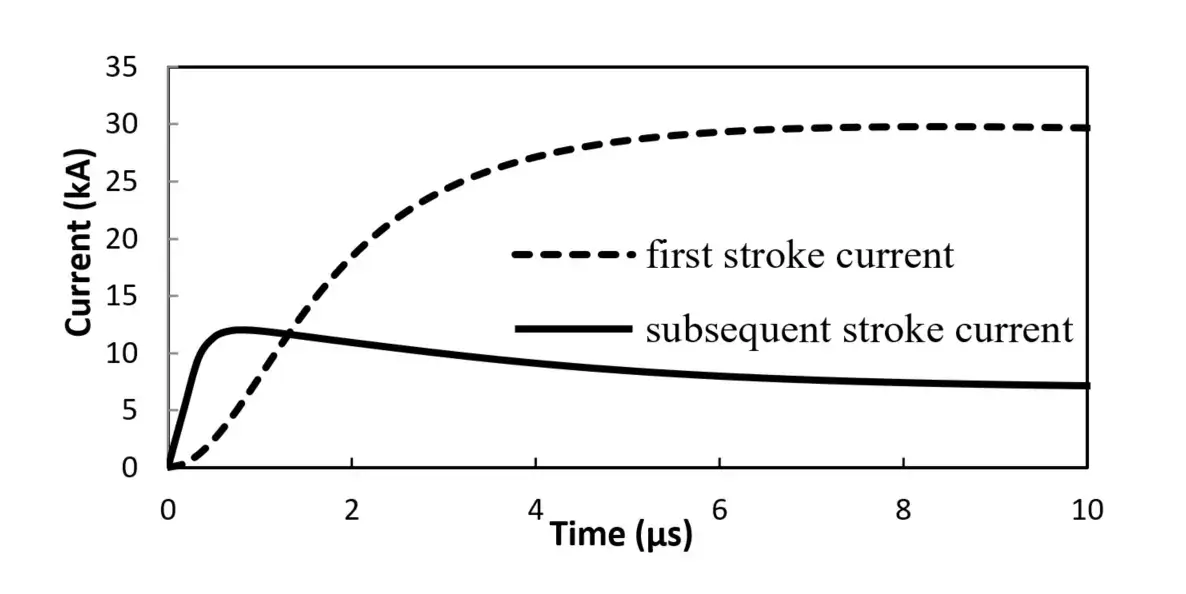
Fig. 6. Formes d'ondes typiques des courants de foudre de retour principal et consécutif

Fig. 7. Impédance d'impulsion d'une tige de mise à la terre verticale soumise à un courant de foudre de retour consécutif présenté à la figure 3.6 [17]

Il est à noter que l'utilisation de plusieurs électrodes de mise à la terre, en particulier à proximité du point d'injection, améliore l'efficacité d'impulsion des systèmes de mise à la terre. Les tiges horizontales sont légèrement moins efficaces à la fréquence du réseau par rapport aux tiges verticales, mais elles ont une meilleure efficacité d'impulsion [17].

Fig. 8. Grille de mise à la terre carrée d1×d2 à espacement égal enterrée à la profondeur h dans un sol avec pertes. Adapté de [14]

Systèmes de mise à la terre complexes

Les systèmes de mise à la terre complexes impliquent généralement une combinaison d'électrodes de mise à la terre verticales et horizontales et peuvent prendre la forme de très grandes grilles de mise à la terre. Les performances transitoires de ces systèmes sont évaluées de manière similaire en utilisant des méthodes électromagnétiques rigoureuses. De manière générale, ces systèmes, similaires au cas des électrodes de mise à la terre simples, présentent un comportement de dépendance en fréquence, en particulier aux hautes fréquences. Pour mieux comprendre le comportement des systèmes de mise à la terre complexes, considérons le cas d'une grille de mise à la terre enterrée dans un sol avec pertes à une seule couche, Fig. 8. La grille de mise à la terre dans ce cas est un carré d1×d2 à espacement égal. La profondeur de la grille est h et les conducteurs ont un rayon r = 12,5 mm. Les performances de la grille de mise à la terre sont obtenues lorsqu'elle est enterrée dans un sol homogène à une seule couche, qui est caractérisé par des conductivités de σ0 = 0,01 S/m, 0,002 S/m, 0,001 S/m et une permittivité relative $\eps_r$ .

L'amplitude et la phase de l'impédance harmonique de la grille de mise à la terre avec h = 0,5 m, d1 = 2 m et d2 = 3 m sont présentées à la figure 9. Comme on peut le voir sur cette figure, l'impédance harmonique prend des valeurs différentes sur l'intervalle de fréquences de travail, présentant un comportement inductif ou capacitif en fonction de la conductivité du sol. La figure 9 montre la tension au point d'injection pour les mêmes systèmes de mise à la terre pour les courants de foudre de retour principal et consécutif de la figure 6.

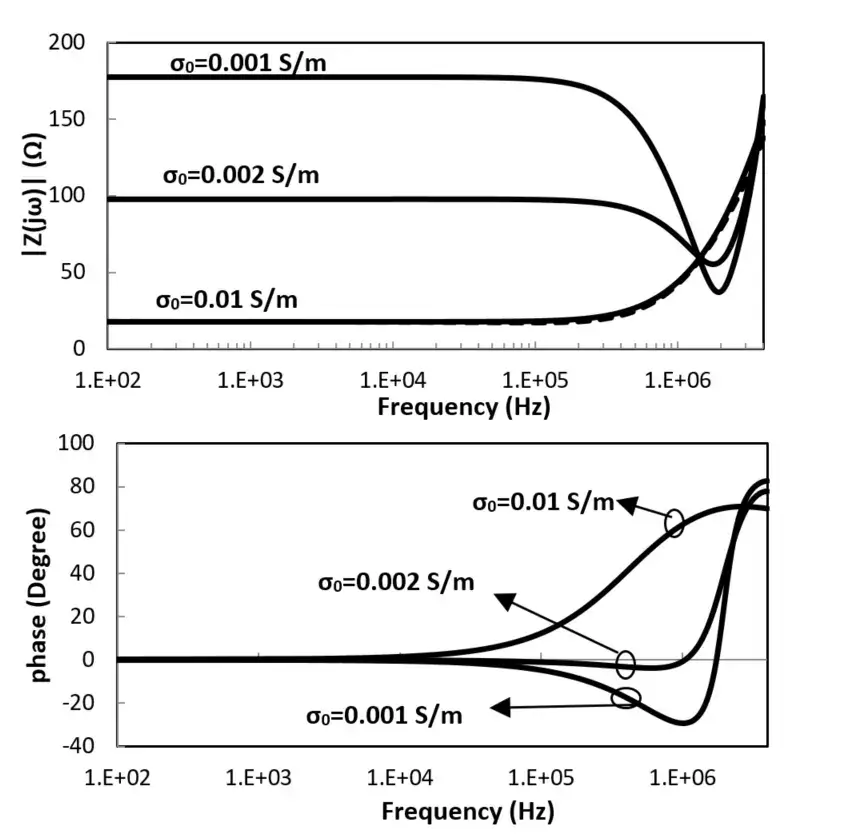
Fig. 9. Impédance harmonique de la grille de mise à la terre présentée à la figure 10, h = 0,5 m, d1 = 3 m, d2 = 2 m enterrée dans un sol avec pertes.

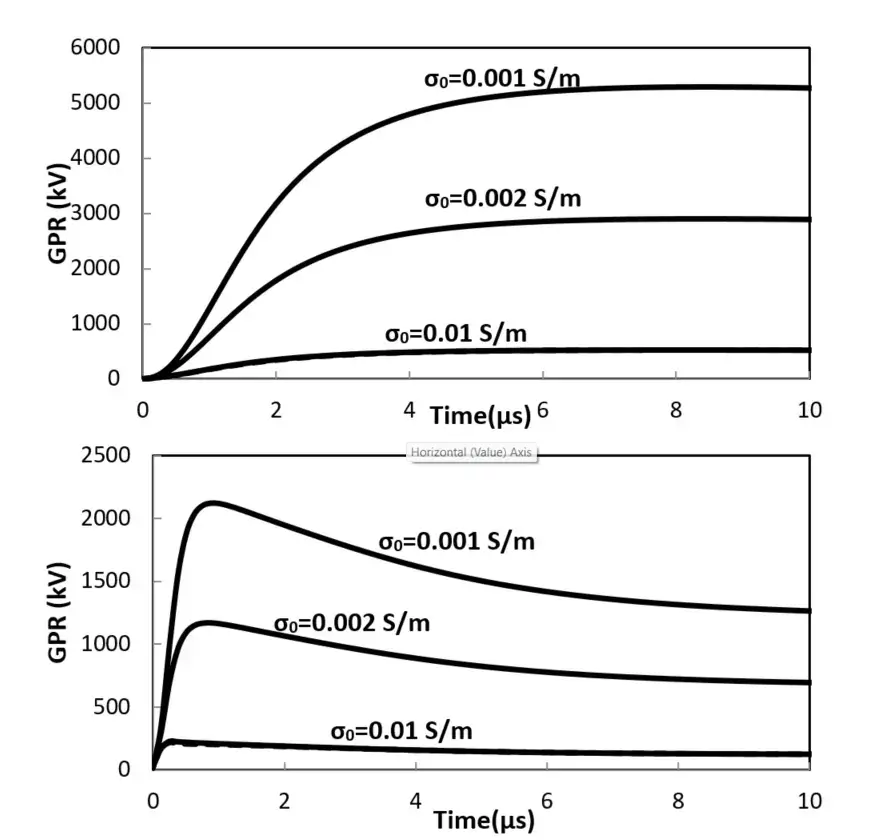
GPR de la grille de mise à la terre présentée à la figure 9, h = 0,5 m, d1 = 3 m, d2 = 2 m soumise à des courants de foudre de retour principal (en haut) et consécutif (en bas).

Fig. 10. GPR de la grille de mise à la terre présentée à la figure 9, h = 0,5 m, d1 = 3 m, d2 = 2 m soumise à des courants de foudre de retour principal (en haut) et consécutif (en bas).

Effet de la dépendance en fréquence des paramètres électriques du sol

La dépendance en fréquence de la conductivité du sol et de la permittivité relative dépend d'une combinaison de facteurs tels que la polarisation des molécules dipolaires, la polarisation de diffusion des ions contraires (due à la séparation des cations et des anions), la polarisation interfaciale (Maxwell-Wagner) ainsi que divers mécanismes de conduction et de perte, chacun agissant sur un intervalle de fréquence spécifique [19]-[23]. En raison de ce fait, la conductivité du sol et la permittivité relative présentent un comportement dépendant de la fréquence sur la plage de fréquences d'intérêt. Par conséquent, l'utilisation d'un modèle précis du sol pourrait contribuer à obtenir une analyse plus précise du comportement transitoire du système de mise à la terre. L'une des modélisations largement utilisées pour modéliser la dépendance en fréquence des paramètres électriques du sol est les formules analytiques proposées par Longmire et Smith [19]. Ces équations se lisent comme suit :

\rho_0 = 125 \cdot (\frac{p}{10})^{-0.54} (\Omega \cdot m), \quad \epsilon_{\infty} = 5

\rho(f) = (\rho_0^{-1} + 2 \pi \epsilon_0 \sum_{n=1}^{14} \frac{a_n (\frac{p}{10})^{1.28 \cdot 10^{n-1}} (\frac{f}{ (\frac{p}{10})^{1.28 \cdot 10^{n-1}}})^2}{1 + (\frac{f}{(\frac{p}{10})^{1.28 \cdot 10^{n-1}}})^2})^{-1}

\epsilon_r(f) = \epsilon_{\infty} + \sum_{n=1}^{14} \frac{a_n}{1 + (\frac{f}{(\frac{p}{10})^{1.28 \cdot 10^{n-1}}})^2}

où f est la fréquence allant de CC à 2 MHz, ρ(f) et εr(f) sont respectivement la résistivité et la permittivité relative du sol, ρ0 est la résistivité basse fréquence, p est le pourcentage d'eau du sol et an sont des coefficients présentés dans le tableau I [19].

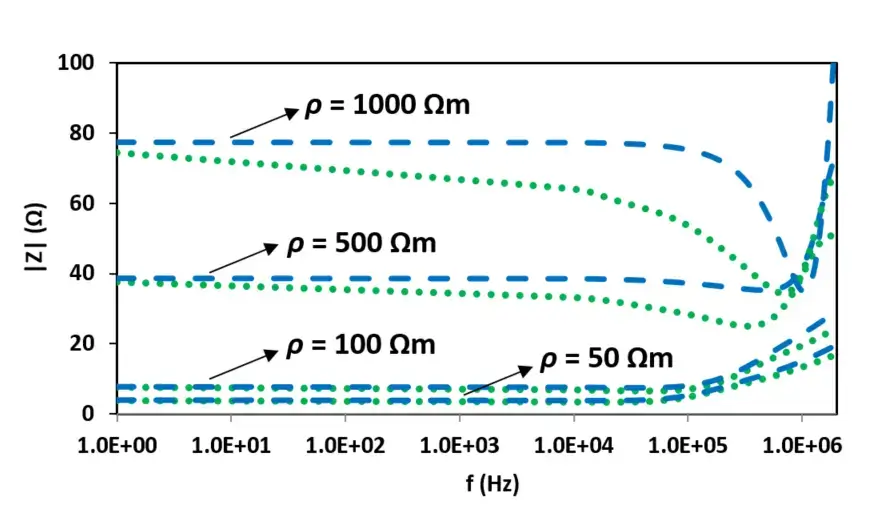
Impédances harmoniques de la tige verticale pour différentes résistivités du sol. Ligne bleue en pointillés : sol avec des paramètres électriques constants, ligne verte en pointillés : sol avec des paramètres électriques dépendants de la fréquence.

Fig. 11. Impédances harmoniques de la tige verticale pour différentes résistivités du sol. Ligne bleue en pointillés : sol avec des paramètres électriques constants, ligne verte en pointillés : sol avec des paramètres électriques dépendants de la fréquence.

La figure 11 montre l'amplitude de l'impédance harmonique de l'électrode de mise à la terre verticale, calculée à l'aide de l'approche MoM présentée dans [24]. L'impédance est calculée dans la plage de fréquences de CC à 2 MHz pour les deux sols avec des paramètres électriques constants et dépendants de la fréquence. De manière générale, la dépendance en fréquence des paramètres électriques du sol pour les sols à forte conductivité peut être raisonnablement ignorée. Néanmoins, pour les sols peu conducteurs (conductivités autour de σ0<=0,002 S/m), la dépendance en fréquence de la conductivité du sol et de la permittivité relative doit être prise en compte pour simuler correctement les performances des systèmes de mise à la terre. Il convient également de noter que l'effet de la dépendance en fréquence des paramètres électriques du sol peut être particulièrement important lorsque les systèmes de mise à la terre sont soumis à des courants de retour consécutifs. Cet effet est beaucoup plus prononcé pour les électrodes longues enterrées dans des sols très résistants.

Fig. 12. Représentation du circuit d'une tige de mise à la terre verticale basée sur les paramètres distribués haute fréquence. Adapté de [32].

Circuits équivalents pour la modélisation haute fréquence des électrodes de terre verticales et horizontales

Un circuit à paramètres distribués peut être utilisé pour représenter adéquatement l'impédance harmonique des tiges de mise à la terre verticales et horizontales [16] et [31]. Dans cette approche, la tige de mise à la terre verticale est divisée en N segments fictifs et chaque segment de la tige est représenté par une section RLC, Fig. 12. Pour chaque segment, les paramètres sont identiques et définis comme suit :

R_n = \frac{\rho N}{2 \pi l} (log \frac{4l}{r} - 1) \quad (\Omega)

C_n = \frac{2 \pi \epsilon l}{N} (log \frac{4l}{r} - 1) \quad (F)

L_n = \frac{\mu_0 l}{2 \pi N} (log \frac{2l}{r} - 1) \quad (H)

où l est la longueur de la tige verticale et r est le rayon. Rn, Ln et Cn sont respectivement la résistance, l'inductance et la capacité de chaque segment. $\rho$ est la résistivité du sol (supposée homogène) en $\Omega$ m, $\mu$ o = 4 $\pi$ 10-7 H/m et $\eps$ est la permittivité du sol (valeur typique : $\eps$ = 10 $\eps$ o avec $\eps$ o = 8,85 × 10-12 F/m).

Les électrodes de terre verticales et horizontales peuvent être modélisées par leur impédance caractéristique et leur constante de propagation, de manière similaire au cas des lignes de transmission. Pour ce faire, les équations (3.7.a) et (3.7.bb) peuvent être utilisées pour la tige verticale [33] et [34] :

Z_c = \frac{A_1}{2 \pi} \sqrt{\frac{j \omega \mu_0 \rho}{(1 + j \omega \epsilon \rho)}}, \quad \gamma = \sqrt{j \omega \mu_0 (1/\rho + j \omega \epsilon)}

et pour la tige horizontale :

Z_c = \frac{A_2}{\pi} \sqrt{\frac{j \omega \mu_0 \rho}{2(1 + j \omega \epsilon \rho)}}, \quad \gamma = \sqrt{j \omega \mu_0 (1/\rho + j \omega \epsilon) / 2}

Par conséquent, en comparaison avec le cas 50 / 60 Hz, où la résistance de mise à la terre peut être simplement calculée pour les tiges verticales et horizontales comme suit :

R_g = \frac{\rho}{2 \pi \ell} A_1, \quad \text{and} \quad R_g = \frac{\rho}{\pi \ell} A_2,

L'impédance de mise à la terre est complexe et dépendante de la fréquence.

Références

[1] IEEE Guide for Safety in AC Substation Grounding, IEEE Std. 80, January-2000.

[2] IEEE Recommended Practice for Grounding of Industrial and Commercial Power Systems (IEEE Green Book). IEEE Std 142 – 1991.

[3] Y. L. Chow and et al.,“ Surface voltages and resistance of grounding systems of grid and rods in two-layer earth by the rapid Galerkins moment method,” IEEE Trans. Power Del., vol. 12, pp. 179-185, Jan. 1997.

[4] Sunde, E. D. 1968. Earth Conduction Effects in Transmission Systems. Dover.

[5] A. F. Otero, J. Cidras, and J. L. Alamo, “Frequency-dependent grounding grid calculation by means of a conventional nodal analysis technology”, IEEE Transactions on Power Delivery, vol. no. 3, pp. 873-877, July 1999.

[6] B. Zhang, J. He, J. B. Lee, X. Cui, Z. Zhao, J. Zou, and S. H. Chang, “Numerical analysis of transient performance of grounding systems considering soil ionization by coupling moment method with circuit theory,” IEEE Transaction on Magnetics, vol. 41, no. 5, pp.1440-1443. MAY 2005.

[7] F. Menter and L. Grcev, “EMTP-based model for grounding system analysis,” IEEE Trans. Power Delivery, vol. 9, no. 4, pp. 1838-1849, Oct. 1994.

[8] L. Yaqing, M. Zitnik, and R. Thottappillil, “An improved transmission line model of grounding system,” IEEE Trans. Electromagn. Compat., vol. 43, no. 3, pp. 348-355, Aug. 2001.

[9] Y. Liu, N. Theethayi, and R. Thottappillil, “An engineering model for transient analysis of grounding grid under lightning strikes: Nonuniform transmission-line approach”, IEEE Transactions on Power Delivery, vol. no. 2, pp. 722-730, Apr. 2005.

[10] L. Qi, X. Cui, Z. Zhao, and H. Li, “Grounding performance analysis of the substation grounding grids by finite element method in frequency domain” IEEE Transactions on Magnetics, vol. 43, no. 4, April 2007.

[11] L. Grcev and F. Dawalibi, “An electromagnetic model for transients in grounding systems,” IEEE Trans. Power Delivery, vol. 5, no. 4, pp. 1773-1781, Nov. 1990.

[12] L. Grcev, “Computation of transient voltages near complex grounding systems caused by lightning currents,” in Proc. IEEE Int. Symp. Electromagn. Compat., 1992, pp. 393-400.

[13] F. Dawalibi and A. Selby, “Electromagnetic fields of energized conductors,” IEEE Trans. Power Delivery, vol. 8, no. 3, pp. 1275-1284, Jul. 1993.

[14] M. Akbari, K. Sheshyekani, and M. R. Alemi, “The effect of frequency dependence of soil electrical parameters on the lightning performance of grounding systems,” IEEE Transactions on Electromagnetic Compatibility, vol. 55, no. 4, pp. 739-746, Aug. 2013.

[15] L. Grcev, “Computer analysis of transient voltages in large grounding systems,” IEEE Trans. Power Delivery, vol. 11, no. 2, pp. 815-823, Apr. 1996.

[16] L. Grcev and M. Popov, “On high-frequency circuit equivalents of a vertical ground rod” IEEE Trans. Power Delivery, vol. 20, no. 2, pp. 1598-1603, Apr. 2005.

[17] CIGRE Working Group C4.4.02, “Protection of MV and LV Networks against Lightning. Part 1: Common Topics”, Paris, 2012.

[18] R. Alipio, S. Visacro, "Frequency Dependence of Soil Parameters: Effect on the Lightning Response of Grounding Electrodes", DOI: 10.1109/TEMC.2012.2210227.

[19] C. L. Longmire and K. S. Smith, “A universal impedance for soils,”Topical Report for Period July 1–September 30, Defense Nuclear Agency, Santa Barbara, California, 1975.

[20] J. H. Scott, “Electrical and magnetic properties of rock and soil,” U.S.Geol. Surv., Dep. of the Interior, Washington, D.C., 1966.

[21] B. D. Fuller, and S. H. Ward, “Linear system description of the electrical parameters of rocks”, IEEE Trans. Geosci. Electron., GE-8 no. 1, pp. 7– 18. Jan. 1970.

[22] R. L. Smith-Rose, “The electrical properties of soils for alternating currents at radiofrequencies,” Proc. Royal Society, vol. 140, no. 841A, pp. 359–377, 1933.

[23] A. C. S. de Lima, and C. Portela, “Inclusion of Frequency-Dependent Soil Parameters in Transmission-Line Modeling”, IEEE Trans. Power Del., vol. 22, no. 1, pp.492-499, Jan. 2007.

[24] M. R. Alemi and K. Sheshyekani, “Wide-band modeling of tower footing grounding system for the evaluation of lightning performance of transmission lines”, IEEE Transactions on Electromagnetic Compatibility, vol. 57, no. 6, pp. 1627-1636, Dec 2015.

[25] A.R. Hileman, “Insulation Coordination for Power Systems,” NewYork: Marcel Dekker, 1999.

[26] F. M. Gatta, A. Geri, S. Lauria, and M. Maccioni, “Generalized pi-circuit tower grounding model for direct lightning response simulation,” Electr. Pow. Syst. Res., vol. 116, pp. 330-337, July 2014.

[27] K. Sheshyekani, M. Akbari, B. Tabei, and R. Kazemi, “Wide-band modeling of large grounding systems to interface with electromagnetic transient solvers,” IEEE Trans. Power Del., vol. 29, no. 4, pp. 1868-1876, Aug. 2014.

[28] CIGRE Working Group 01 (Lightning) of Study Committee 33 (Overvoltages and Insulation Co-ordination), “Guide to procedure for estimating the lightning performance of transmission lines,” Document 63, Oct. 1991.

[29] P. Chowdhuri, J. G. Anderson, W. A. Chisholm, T. E. Field, M. Ishii, J. A. Martinez, M. B. Marz, J. McDaniel, T. R. McDermott, A. M. Mousa, T. Narita, D. K. Nichols, and T. A. Short, “Parameters of lightning strokes: a review,” IEEE Trans. Power Del., vol. 20, no. 1, pp. 346-358, Jan. 2005.

[30] F. H. Silveira, S. Visacro, A. De Conti, and C. R. de Mesquita, “Backflashovers of transmission lines due to subsequent lightning strokes,” IEEE Trans. Electromagn. Compat., vol. 54, no. 2, pp. 316-322, April 2012.

[31] C. T. Mata, M. I. Fernandez, V. A. Rakov, and M. A. Uman, “EMTP modeling of a triggered-lightning strike to the phase conductor of an overhead distribution line,” IEEE Trans. Power Delivery. vol. 15, no. 4, pp. 1175–1181, Oct. 2000.

[32] K. Sheshyekani, S.H. H. Sadeghi, R. Moini, F. Rachidi and M. Paolone, “Analysis of Transmission Lines with Arrester Termination, Considering the Frequency-Dependence of Grounding Systems”, IEEE Transactions on Electromagnetic Compatibility, vol. 51, no. 4, pp. 986-994, Nov. 2009.

[33] S. Ramo, J. R. Whinnery, and T. van Duzer, Fields and waves in communication electronics, 3 ed. New York: Wiley, 1994.

[34] L. Grcev and V. Arnautovski, "Comparison between simulation and measurement of frequency dependent and transient characteristics of power transmission line grounding," presented at 24th International Conference on Lightning Protection (ICLP'98), Birmingham, U.K., 1998